|
Барвинский И.А.
(Компания CSoft)
III
Международный семинар «Современные
технологии литья пластмасс. Локализация
производства автокомпонентов и
проблемы контроля качества». Санкт-Петербург.
15-16 сентября. 2011. С. 1-28.
Аннотация
Для решения задачи локализации
производства литьевых автомобильных
деталей из термопластов необходимо
обеспечить их размерную точность в
соответствии с КД при желательном
использовании отечественного
полимерного сырья. Проблема точности
размеров связана с необходимостью
прогнозирования усадочного поведения
литьевых деталей для определенных
марок термопластов. Прогнозирование
усадки относится к сложным задачам из-за
неравномерности усадочных процессов и
их зависимости от конструктивных
особенностей литьевой детали и формы,
технологического режима литья,
материала детали и других условий. В
докладе рассмотрены факторы,
определяющие усадку термопластов при
литье под давлением, а также способы
прогнозирования усадки на основе
традиционных подходов и
математического моделирования с
использованием численных методов.
Линейная усадка является
одной из характеристик напряженно-деформированного
состояния отливки, возникающего в
результате объемной усадки при влиянии
процессов ориентации (макромолекул
полимера, наполнителя или дисперсной
фазы в полимерных смесях и некоторых
сополимерах), а также условий
вязкоупругой релаксации отливки в
форме и при ее извлечении из формы и т.д.
В традиционных подходах к
прогнозированию усадки используются
значения усадки, определяемые в
соответствии с ГОСТ 18616-80, ИСО 294-4, ASTM D 955 и др. стандартами. Обычно это
приводит к необходимости доработок
формы из-за отклонений усадки от
стандартных значений ввиду различных
условий литья, реализуемых в формах для
стандартных образцов и реальных
изделий. Для снижения затрат и
сокращения сроков изготовления
оснастки применяются прототипы
литьевых деталей и форм.
Развитие моделирования
процесса литья термопластов открывает
новые возможности для решения проблем
усадки. В докладе обсуждаются методы
прогнозирования линейной усадки,
применяемые в современном
компьютерном анализе: метод «остаточных
деформаций» (residual strain) и варианты метода «остаточных
напряжений» (residual stress).
1.
Усадочные процессы при литье
термопластов
1.1. Объемная усадка
Первопричина
размерных изменений отливки при литье
термопластичных материалов,
называемых усадкой, заключается в
изменении объема отливки при ее
охлаждении. Так как обычно объем
отливки меньше объема полости, говорят
об объемной усадке (volumetric shrinkage, volume shrinkage)
термопластичного материала [1-7].
Выраженная в процентах
объемная усадка Sv составляет [3]:
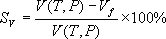 ,
(1) ,
(1)
где V(T, P) – средний
удельный объем расплава (величина,
обратная плотности расплава) при
температуре и давлении расплава в
полости, Vf –
средний удельный объем полимерного
материала при комнатной температуре и
атмосферном давлении. При таком
определении объемной усадки ее можно
легко рассчитать на основе PVT-данных,
если известны давление и температура
расплава в полости формы (см. раздел 3.1).
В
альтернативном методе объемная усадка
определяется как относительное
изменение объема отливки (vpart)
после ее охлаждения до комнатной
температуры по сравнению с объемом
полости формы (vmold) [2-3, 8-9]:
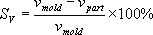 (2)
(2)
Большое влияние на
объемные изменения кристаллизующихся
термопластичных материалов,
характеризуемые PVT-диаграммой,
оказывают скорость охлаждения и
течение расплава [10]. Снижение скорости охлаждения
приводит к увеличению степени
кристалличности полимера и,
соответственно, к снижению удельного
объема твердого полимера и увеличению
объемной усадки. Течение также
способствует увеличению степени
кристалличности полимера и объемной
усадки из-за явления ориентационной
кристаллизации [11-12].
Добавление
минеральных, стеклянных и других
неорганических наполнителей снижает
объемные изменения, отражаемые на PVT-диаграмме, т.к. уменьшает
содержание полимерного материала в
композиции. Ряд веществ, добавляемых в
малых количествах, могут оказывать
влияние на процесс кристаллизации (выполняя
роль зародышей кристаллизации) и,
соответственно, на объемные изменения
при охлаждении. Известно много добавок
такого рода, называемых нуклеаторами
или структурообразователями, в их
число входят, например, некоторые
пигменты [13].
Объемная усадка для
конкретной марки термопластичного
материала при литье под давлением
изменяется в широких пределах в
зависимости от технологического
режима и рассматриваемой области
детали.
После заполнения формы на стадии
уплотнения (подпитки) под действием
давления выдержки происходит
увеличение массы находящегося в
литьевой полости полимерного
материала, что позволяет частично
скомпенсировать уменьшение объема
отливки, вызванного охлаждением.
Повышение давления выдержки или
времени выдержки под давлением (вплоть
до момента отключения полости от
материального цилиндра) приводит к
снижению объемной усадки.
Объемную усадку, широко
применяемую при расчетах процесса
литья, сложно измерить
экспериментально на реальных деталях
из-за потери монолитности отливки с
образованием внутренних усадочных
полостей, микропористой или
макропористой структуры ее внутренней
части.
При отрицательной
объемной усадке (когда объем области
отлитой детали превышает объем
соответствующей части полости) отливку
из большинства полимерных материалов
невозможно извлечь из обычных форм [7], а
значит невозможно измерить ее объем.
Исключением являются термопластичные
эластомеры, имеющие низкую твердость,
которые могут извлекаться из формы и
при отрицательной объемной и линейной
усадке [14]. При очень высокой объемной
усадке происходят большие искажения
геометрии детали.
Линейная усадка является
одной из характеристик напряженно-деформированного
состояния отливки, возникающего в
результате объемной усадки при влиянии
различных факторов. Рассмотрим
основные факторы, определяющие
напряженное состояние и деформации
отливки в форме, а также при
выталкивании и после извлечения
отливки из формы.
1.2. Напряжения и деформации
отливки в форме
Пока отливка
находится в закрытой форме, в ней
формируется напряженное состояние,
основной вклад в которое вносят
термические напряжения (thermal stresses, thermally-induced stresses) - напряжения,
вызванные градиентами температуры в
процессе охлаждения в сочетании с
быстрым повышением жесткости
полимерного материала при его
затвердевании [15-17].
Одним из факторов,
определяющих температурные градиенты
в отливке, является температура
расплава, поступающего в литьевую
полость из материального цилиндра
через литниковую систему. Температура
расплава зависит от температуры дозы
впрыска в передней части материального
цилиндра, а также от теплового баланса
в литниковой системе и полости формы.
Для литья
термопластичных материалов характерна
высокая неравномерность температуры в
дозе расплава вследствие
периодической шнековой пластикации [18-19], а также повышение
температуры в дозе расплава при
впрыске из-за влияния адиабатического
сжатия расплава [20-21].
Большое влияние на
тепловой баланс расплава в литниковой
системе (холодноканальной или
горячеканальной) и полости формы
оказывает диссипация тепла при
сдвиговом течении [22].
Диссипация увеличивается при
повышении скорости течения расплава и
уменьшении толщины (диаметра)
литникового канала или полости.
Разветвления литниковых каналов могут
быть причиной повышения
неравномерности температуры расплава,
поступающего в полость формы [23].
Другой фактор,
определяющий градиенты температуры в
отливке, - тепловой поток от формующей
поверхности, который в свою очередь
зависит от конструкции системы
охлаждения формы, материалов ФОД,
хладагента, его температуры и скорости
течения в охлаждающих каналах [5, 24] и
прочего. Скорость охлаждения отливки
уменьшается при образовании
воздушного зазора между отливкой и
формующей поверхностью в процессе
усадки по толщине [25-26].
Большое влияние на напряженное
состояния отливки оказывает
распределение давления в полости формы
и его изменение во времени на стадии
уплотнения. В частности, благодаря
условиям, реализуемым на стадии
уплотнения, при литье термопластов под
давлением формируются характерные
эпюры остаточных напряжений с
растягивающими напряжениями в
поверхностном слое отлитой детали [16-17].
Иногда, подчеркивая влияние давления
на термические напряжения, говорят о «напряжениях,
вызванных давлением» (pressure-induced stresses) [27-28].
Анизотропия усадочных процессов, т.е.
зависимость усадки от направления
измерений (различают продольную и
поперечную усадку) связана с влиянием
ориентационных напряжений, которые
могут иметь различную природу.
«Замороженные» (frozen-in)
ориентационные напряжения возникают в
застывшем поверхностном слое
полимерной детали, образующемуся к
моменту окончания стадии заполнения.
Хотя по величине эти напряжения на
порядок меньше термических [15-16], они
приводят к анизотропии механических и
усадочных и свойств и оказывают, тем
самым большое влияние на процессы
усадки.
Традиционно предполагается, что свой
вклад в молекулярную ориентацию в
поверхностном слое вносят деформации
растяжения расплава при его течении на
фронте потока (фонтанном течении) и
сдвиговое течение [29-30]. Однако в работе [31] было показано, что при литье пластины из
полистирола влияние фонтанного
течения на ориентацию поверхностного
слоя незначительно.
Формирование пристенного слоя
происходит на стадии заполнения в
условиях высоких скоростей течения и
охлаждения, т.к. поверхностный слой
контактирует с металлической стенкой
формы, обладающей высокой
теплопроводностью. Более глубокие слои
литьевой детали застывают на стадиях
выдержки под давлением и выдержки на
охлаждение при сравнительно невысоких
скоростях течения расплава или в
отсутствие течения и сравнительно
медленном охлаждении. Тем не менее,
внутренние слои могут иметь высокие
ориентационные напряжения,
достигающие или даже превышающие
напряжения поверхностных слоев, что
объясняется совместным влиянием ряда
факторов, в том числе снижением
скорости релаксации вблизи
температуры стеклования [32-33].
В работах [34-35]
показано, что ориентация центральной
части литьевой детали может появляться
и вследствие ее охлаждения без течения.
Таким образом, ориентационные
напряжения могут быть частью
термических напряжений.
На анизотропию
напряженного состояния отливки в форме
и результирующую усадку влияют [6] явления анизотропии теплопроводности
расплава при его течении [36] и (для
кристаллизующихся материалов)
ориентационная кристаллизация при
сдвиговом или элонгационном течении.
Вязкоупругая
релаксация [37-38] приводит к снижению
напряженного состояния отливки,
находящейся в закрытой форме, и
соответственно к меньшей усадке после
извлечения отливки из формы. Локальное
напряженное состояние отливки
снижается при образовании внутренних
усадочных полостей или пористой
структуры.
Обратимые деформации
формы под действием давления,
создаваемого расплавом в литьевой
полости [39], а также под действием
усилия запирания литьевой машины
оказывают существенное влияние на
напряженное состояние отливки в форме
и результирующую усадку.
Традиционно линейная
усадка подразделяется на свободную и
несвободную. Предполагается, что
свободная усадка наблюдается в том
случае, когда «оформляющие части формы
не препятствуют усадке материала» [40],
т.е. свободная усадка происходит, пока
отливка находится в форме. В последнее время
проблема линейной усадки в закрытой
форме вызывает большой интерес
исследователей [41-45].
Очевидно, что для
некоторых размеров усадка в форме
вообще невозможна из-за геометрических
ограничений, например, усадка на
отверстии происходит только после
извлечения знака, формующего это
отверстие. В общем случае время начала
и величина линейной усадки в форме
определяется зависящим от условий
процесса балансом сил, способствующих
усадке (сил контракции вследствие
объемной усадки) и препятствующих
усадке (сил, вызванных сцеплением
отливки с формующей поверхностью)
[46].
На сцепление отливки с
формой очень большое влияние оказывает
шероховатость и текстура формующей
поверхности. Обычно даже при глянцевой
формующей поверхности лицевой части
литьевых деталей, формующая
поверхность обратных частей имеет
высокую шероховатость, что
обеспечивает хорошее сцепление
отливки с формой. В работе [47] линейная
усадка (после извлечения из формы)
пластины из полипропилена для полости
с гладкими формующими поверхностями
составила 1.99%, тогда как для полости, у
которой одна из формующих поверхностей
являлась гладкой, а другая имела
высокую шероховатость, усадка была
равна 1.45%. Для полистирола общего
назначения в аналогичных условиях
усадка составила соответственно 0.67% и
0.55%.
В работе [45] процессы
усадки изучались экспериментально и
путем моделирования для отливки в виде
пластины из сополимера полипропилена,
содержащего небольшое количество
талька. Разница между продольными
усадками, определяемыми как свободная
и затрудненная, уменьшалась при
повышении давления выдержки, причем
при давлении выдержки, превышающем 50
МПа, свободная и затрудненная усадки
практически были равны.
Таким образом, можно
предположить, что понятие свободной
усадки относится к условиям, которые
реализуются при недостаточном
уплотнении, когда высокая усадка в
направлении толщины [48] дает
возможность для линейной усадки в
форме. При хорошем уплотнении отливка
имеет сильное сцепление с формующей
поверхностью, в том числе за счет
коробления в форме [49], что препятствует
линейной усадке в форме. При хорошем
уплотнении усадка в форме даже для
предельно простой конструкции
литьевой детали возможна только в
направлении толщины. Данный вывод
относится к материалам, имеющим малую и
среднюю жесткость. Материалы с высокой
жесткостью, например, термопласты,
наполненные стеклянным или углеродным
волокном, отличаются очень высоким
уровнем напряженного состояния
отливки в форме, что, возможно,
оказывает влияние на специфику их
усадочного поведения.
1.3. Напряжения и деформации
отливки при извлечении из формы
В процессе
извлечения отливки из формы возникают
дополнительные напряжения (ejection-indused
stresses), обусловленные механическим
взаимодействием отливки и деталей
формы при выталкивании [50].
Изменение геометрии детали и
снижение ее напряженного состояния в
начальный период после ее извлечения
из формы связывают с почти мгновенным
процессом упругого восстановления (elastic
recovery) [51] и
сравнительно медленным процессом
вязкоупругой релаксации (см., например, [52]).
Деформации и напряженное состояние
отливки после извлечения из формы
зависят от механических характеристик
отливки. Условия охлаждения в форме,
изменение режима скорости течения и
давления определяют формирование
слоевой структуры деталей, которая
наблюдается в частности для
кристаллизующихся полимерных
материалов
[53-54,
12]. Литьевая деталь может
рассматриваться как слоистый композит,
свойства которого, например, модуль
упругости, изменяется в направлении
толщины детали [55].
Для материалов, содержащих жесткие
волокнистые наполнители, такие как
стекловолокно или углеродное волокно,
механические свойства значительно
изменяются, как по длине-ширине, так и в
направлении толщины детали, что
обусловлено изменением ориентации
наполнителя [56].
Слоевая структура характерна также
для привитых сополимеров, блок-сополимеров
и несовместимых смесей полимеров, в
которых один из компонентов образует
дисперсную фазу. Различная ориентация
частиц дисперсной фазы [57-58] в слоях
отливки определяет различия в их
механических свойствах, что может
оказывать влияние на усадочные
процессы в подобных материалах. К
материалам такого рода можно отнести, в
частности эластифицированные
термопласты, содержащие дисперсную
каучуковую фазу.
При сравнении геометрии отлитой
детали с геометрией литьевой полости
традиционно различают, главным образом
по методам измерения, линейную
технологическую усадку (processing
shrinkage,
molding shrinkage, mold
shrinkage, as-molded
shrinkage
[17]), называемую просто усадкой, к
которой относят деформации,
обусловленные линейным уменьшением
размеров, и коробление (warpage)
- деформации, которые характеризуют
искажение формы отливки. При этом часть
напряженного состояния отливки
сохраняется в виде остаточных
напряжений.
Из-за влияния
вязкоупругости и других факторов (см.
ниже) значительные размерные изменения
детали происходят в течение некоторого
времени после извлечения детали из
формы. По этой причине замеры деталей,
сделанные сразу после литья, не всегда
являются корректными, хотя предыдущие
издания стандарта ASTM
D955 (например, издание 2000 года)
допускали измерения деталей в течение
одного часа после извлечения из формы с
определением «начальной» усадки (initial
shrinkage). Текущее издание данного
стандарта [59] предусматривает
измерения усадки только через 24
+/- 0.5 и 48
+/- 0.5 часов после литья.
Для большинства
полимерных материалов обычно
рекомендуется проводить измерения
размеров деталей через 16-24 часов после
литья, что соответствует ГОСТ 18616-80 [60],
однако в некоторых случаях, например,
для термопластичных эластомеров этот
период увеличивают до 40-48 часов [61].
Медленные процессы
изменения размеров и напряженного
состояния литьевых полимерных деталей,
обусловленные вязкоупругими
свойствами и физическим старением
материала, могут происходить в течение
месяцев или даже лет после их
изготовления. На размерные изменения
влияют различные процессы, связанные с
изменением структуры (например, при
вторичной кристаллизации [62]
кристаллизующихся полимеров), влиянием
влажности и различных факторов внешней
среды. Долговременное изменение
линейных размеров деталей в условиях
хранения или эксплуатации называют
эксплуатационной усадкой [63].
В стандартах [60, 64]
описаны методы определения
дополнительной усадки (post-molding shrinkage)
после выдерживания отлитых образцов
при повышенной температуре. В данных
стандартах указано, что условия
термообработки в таких испытаниях
должны быть взяты из соответствующих
стандартов на материал или согласованы
заинтересованными сторонами.
Необходимо учитывать, что испытания
такого рода не отражают
долговременного усадочного поведения
реальных литьевых деталей, в частности
из-за различий напряженного состояния
реальных деталей и образцов, а также
влияния условий испытаний. Например, в
работе [65] отмечается, что размерные
изменения деталей из аморфных
полимерных материалов при
температурах, превышающих температуру
стеклования, в общем, не характеризуют
изменения размеров при температурах
ниже температуры стеклования.
Напряженное состояние и деформации
(в том числе, линейная усадка), имеющие
различные значения в разных областях
отливки, зависят от конструкции
литьевой детали и формы,
технологического режима литья,
особенностей поведения применяемой
марки полимерного материала.
Молекулярная ориентация полимера в
процессе литья, а также ориентация
волокнистых наполнителей являются
причинами анизотропии усадки,
проявляющейся в разнице значений
продольной и поперечной усадки (в этом
случае усадку называют анизотропной).
Для материалов с
дисперсными наполнителями (минеральными
и др.) неравномерность распределения
напряженного состояния и усадки в
детали может быть связана с
неравномерным распределением
наполнителя [66].
Для материалов с жесткими волокнистыми
наполнителями (стекловолокно,
углеродное волокно и т.д.)
неравномерность напряженного
состояния и усадки также повышается
при увеличении неравномерности
распределения длины волокна
вследствие разрушения частиц волокна в
процессе переработки [67-68].
Сложность явлений,
влияющих на напряженно-деформированное
состояние отливки в форме и после
извлечения из формы, а также
разнообразие применяемых полимерных
материалов обусловливают сложность
прогнозирования усадки для конкретных
деталей.
2.
«Традиционные» подходы к
прогнозированию усадки
2.1. Прогнозирование линейной
усадки на основе стандартных значений
В отечественной
практике прогнозирование линейной
усадки (далее – усадки) деталей чаще
всего производится [63] на
основе значений усадки, определяемых
на специальных образцах по ГОСТ 18616-80
[60]. В этом стандарте для измерения
усадки используются образцы в форме
брусков и дисков. Изменение № 2 данного
стандарта, действующее с 2005 года,
предусматривает также применение
образцов в виде прямоугольных пластин
60 х 60 мм, аналогичных тем, которые
рекомендуют стандарты [59, 64]. Стандарты
[59-60, 64] включают методы определения
продольной (в направлении длины
образца) и поперечной (в направлении
ширины образца) усадки. Анизотропия
усадки в [60] определяется как
отношение
поперечной усадки к продольной.
Методика
расчета размеров ФОД с использованием
минимальных, максимальных или средних
значений усадки для диапазона
колебания усадки рассмотрена, например,
в [69], а также в работах
[63, 70-72].
В
стандартах по усадке указано, что они
разработаны «для получения
сопоставимых данных на стандартных
образцах» [59], оценке «типичного
поведения» [64] полимерного материала и
не предназначены для прогнозирования
значений усадки реальных литьевых
деталей. Аналогичные разъяснения были
даны разработчиками ГОСТ 18616-80 [73].
Поэтому, например, в стандарте на метод
расчета исполнительных размеров ФОД [69]
нет ссылок на метод определения усадки
по ГОСТ 18616-80.
Различия усадки
полимерного материала на стандартных
образцах и усадки реальных деталей
обусловлено различным напряженным
состоянием образцов и реальных деталей
в форме и после их извлечения из формы,
что связано с совместным влиянием
конструктивных и технологических
факторов [74].
Важнейшими
конструктивными факторами, влияющими
на усадку, является толщина полости,
длина затекания в полости и
конструкция литниковой системы.
Увеличение толщины образцов при тех же
условиях в большинстве случаев
приводит к увеличению усадки (см.,
например, [5]), хотя известны примеры
более сложного усадочного поведения
при повышении толщины: с минимумом [75]
или максимумом [76].
В работе [77] показано, что продольная
усадка марок термопластичных
эластомеров (на основе смеси
полипропилена и СКЭПТ с динамической
вулканизацией) изменяется при
увеличении толщины образца с минимум, а
поперечная – с максимумом.
Для постоянного
давления выдержки с увеличением длины
затекания увеличивается
неравномерность усадки. Обычно
предполагается, что для деталей равной
толщины усадка повышается при
увеличении расстояния от впуска, т.к. в
том же направлении уменьшается
максимальное (в цикле литья) давление
расплава в полости формы [5]. Применение
профиля давления выдержки со снижением
давления позволяет уменьшить
неравномерность усадки.
Условия уплотнения в
реальных формах могут очень сильно
отличаться от условий, реализуемых в
формах на образцы. Например, при
использовании тонких впускных
литниковых каналов, давление в полости
формы быстро снижается после
застывания впускного литника, что
ведет к повышению усадки и увеличивает
ее неравномерность. Впуск в тонкую
часть полости приводит к значительному
увеличению разброса усадки по длине
детали, причем влияние уменьшенной
толщины в области впуска на разброс
усадки в полости может быть гораздо
больше влияния длины затекания.
Определенные проблемы
связаны с применением понятий
продольной и поперечной усадки к
реальным деталям из-за сложного
характера деформирования расплава при
заполнении формы (в большинстве
случаев расплав имеет двухосную
молекулярную ориентацию), а также из-за
изменения направления течения в
процессе заполнения формы.
Различное усадочное
поведение стандартных образцов и
реальных деталей вызывает
необходимость доработок ФОД после
проведения испытаний. В этом случае
литьевая форма выполняет функцию
прототипа (опытной формы), размеры
которого корректируются после
испытаний на основании измерения
фактической усадки.
2.2. Применение прототипов
деталей и форм
Доработка
литьевой формы после испытаний –
широко распространенная практика,
которая ведет к нежелательному
удлинению периода изготовления формы,
дополнительным затратам, а порой и к
уменьшению ресурса работы формы [74].
Одним из методов снижения
затрат и сокращения сроков
изготовления формы является
применение прототипов (опытных деталей)
[7, 78], воспроизводящих
основные элементы конструкции детали (толщину,
длину затекания и др.), но не содержащих
мелких элементов. Такие прототипы
широко применяются, например, при
изготовлении форм для литья зубчатых
колес [79].
Типичный подход предусматривает
предварительное измерение фактической
усадки на отливках, полученных в форме
с ФОД без зубчатого венца.
Преимуществом
специализации изготовителей форм на
определенных видах литьевых деталей
является возможность использования
информации об усадочном поведении
материалов при проектировании форм для
аналогичных деталей. В этом случае
предыдущие проекты играют роль
прототипов.
На протяжении всего
периода научного изучения проблемы
усадки термопластов при литье под
давлением делались попытки разработки
образцов более сложной конструкции -
своеобразных унифицированных
прототипов литьевых деталей - которые
можно было бы применять для получения
информации по усадкам для
использования при проектировании
реальных форм на различные детали.
Соответствие усадочного
поведения прототипа реальной детали
определяется соответствием условий
формирования напряженно-деформированного
состояния отливки в форме и после ее
извлечения из формы. Выбор
конструктивных факторов, влияющих на
усадку конкретной детали, а также
обоснование возможности применения
прототипа при прогнозировании усадки
может быть сделано статистическими
методами. При выборе прототипа
необходимо учитывать, что влияние
положения впуска и конструкции
литниковой системы на усадку может
быть больше, чем влияние конструкции
литьевой детали. Поэтому в общем случае
правильнее говорить о прототипе
литьевой формы.
При оценке усадки на
прототипах форм необходимо обращать
внимание на материалы ФОД, время цикла
[78], текстуру формующей поверхности и
другие факторы, изменение которых
может привести к изменению усадки.
Оценка применимости того или другого
прототипа для прогнозирования усадки
детали может быть выполнена с
использованием компьютерного анализа.
Для получения сравнительно
небольших партий деталей широко
применяются литьевые формы с ФОД из
алюминиевых сплавов, композитов на
основе полимерных материалов и др.
Литье деталей из термопластов в таких
формах имеет свои особенности,
отличающие его от процесса литья в
обычных формах, в частности по давлению
в форме, условиям охлаждения отливок и
т.д. Например,
для ФОД из композитных материалов на
полимерной основе процесс литья
осуществляют при сравнительно
небольшом давлении выдержки, т.к.
повышение давления выдержки может
привести к разрушению оснастки. По этой
причине усадка деталей, полученных в
таких формах, обычно существенно
превышает усадку деталей, отливаемых в
обычных формах [80-82].
2.3. Учет влияния конструкции
детали и формы, технологического
режима на усадку
В
эмпирическом подходе учет влияния толщины детали,
длины затекания и других
конструктивных факторов на усадку
производится путем корректировки
значений усадки на основе
экспериментальных данных.
Рекомендации по оценке влияния
конструктивных факторов на усадку
приводятся, например,
в работах [8-9, 70, 78].
В работе [83]
рассмотрен метод оценки усадки
термопластичных полиэфирных
эластомеров на основе усадки,
определенной экспериментально на
образце толщиной 3.2 мм в «стандартных»
условиях (при давлении впрыска 70 МПа и
температурах формы и расплава,
соответствующих средним значениям
рекомендуемого диапазона переработки).
Для учета влияния толщины, давления
формования, температуры формы, времени
выдержки под давлением применяются
зависимости вида «изменение усадки –
параметр». Отмечается, что данный метод
может применяться для грубой оценки
усадки.
2.4. Оценка изотропной усадки на
основе PVT-диаграммы
При одинаковой
усадке во всех направлениях линейная
усадка связана с объемной усадкой,
выраженной в долях, соотношением [84]:
Sis =
1 – (1 - Sv)1/3 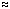 1/3
Sv,
(3) 1/3
Sv,
(3)
где приближенная оценка получена
путем разложения кубического корня в
ряд Тейлора при ограничении разложения
вторым членом ряда. Определенную таким
образом усадку Sis называют
изотропной (isotropic shrinkage). Изотропную усадку области
детали можно оценить (при известном
распределении давления и
среднеобъемной температуры в полости)
исходя из PVT-диаграммы по формулам (1) и (3)
[85].
В литературе термин «изотропная
усадка», применяется и в других
значениях. Часто под изотропной
усадкой понимают усадку в отсутствие
анизотропии, т.е. при равенстве
продольной и поперечной усадки. В таком
подходе об усадке в направлении
толщины может быть вообще ничего не
известно, хотя она обычно намного
превышает продольную и поперечную
усадку (при сохранении монолитности
отливки), поскольку является свободной.
В работе [86]
расчет усадки по выражению (4) для
ненаполненных марок ПБТ показал
отклонение в пределах 30% от
экспериментальных значений. Для ПБТ,
наполненных стекловолокном, ошибка
прогнозирования усадки увеличивалась
более чем в два раза.
3.
Прогнозирование усадки в компьютерном
анализе
Развитие
моделирования литья термопластов с
использованием численных методов
привело к созданию новых подходов к
прогнозированию усадки. Компьютерный
анализ литья термопластов с помощью
коммерческих программных продуктов
позволяет смоделировать стадии
заполнения, уплотнения, охлаждения в
форме и получить информацию о
поведении полимерного материала в
полости формы (распределения
температуры, давления, ориентация и др.),
необходимую для прогнозирования
напряженно-деформированного состояния
отливки, в частности ее усадки.
Прогнозирование усадки в
компьютерном анализе выполняется с
учетом ряда упрощений и допущений,
определяемых применяемыми методом
анализа (2.5D или 3D), моделями отливки (сетки),
условий процесса литья, материала
детали (модели реологического,
теплофизического, механического
поведения и прочие) и др. [87]. В частности
предполагается отсутствие деформаций
отливки в форме до ее раскрытия (кроме
усадки в направлении толщины),
отсутствие обратимых деформаций формы
под действием давления в полости и
усилия запирания (тепловое расширение
полости может учитываться в анализе), а
также одновременное устранение
геометрических ограничений при
раскрытии формы.
Как было отмечено выше, для
материалов, наполненных волокном,
усадочные процессы зависят от
ориентации волокна в детали. Расчет
ориентации жесткого волокнистого
наполнителя может быть выполнен в
программных продуктах Autodesk Moldflow 2012 с использованием моделей
Фольгара-Такера [88] и RSC (Reduced strain closure)
[89] для короткого волокна и модели ARD
(Anisotropic rotary diffusion) [90] – для длинного волокна.
Методология расчета ориентации
волокнистого наполнителя рассмотрена
в работах [27, 91].
Влияние
конструкции охлаждающих каналов и
технологического режима охлаждения на
усадку может быть учтено при
выполнении анализа охлаждения формы.
Ниже рассмотрены методы
расчета объемной и линейной усадки,
реализованные в программных продуктах Autodesk Moldflow 2012 [92].
|





